11. Container With Most Water

11. Container With Most Water (Medium) 盛最多水的容器

题干

You are given an integer array height of length n. There are nvertical lines drawn such that the two endpoints of the ith line are (i, 0) and (i, height[i]).

Find two lines that together with the x-axis form a container, such that the container contains the most water.

Return the maximum amount of water a container can store.

Notice that you may not slant the container.

Example 1:

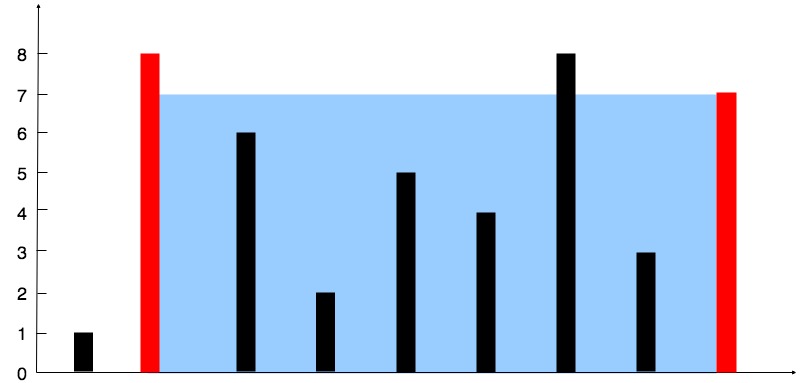
Input: height = [1,8,6,2,5,4,8,3,7]
Output: 49
Explanation: The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

Example 2:

Input: height = [1,1]
Output: 1

Constraints:

• n == height.length
• 2 <= n <= 105
• 0 <= height[i] <= 104

解法思路

我的解法

双指针，指向左右两根柱子，移动较短的那根柱子。

面积等于index之差*短柱子，index从大到小循环，那只有移动较短的那根柱子，才有可能面积更大；

假设移动的不是短柱子，是长柱子，假设下一个元素大于短柱子，那么对面积增加毫无帮助。假设下一个元素小于短柱子，那么对面积增加毫无帮助。

优化解法

移动短柱子时，因为index减少，所以只有下一个元素大于短柱子，才需要计算。理论上在计算之前对比新旧柱子高度即可节省计算。

答案

我的答案

class Solution:
    def maxArea(self, height: List[int]) -> int:
        cur_area = 0
        max_area = 0
        left = 0
        right = len(height) - 1
        while left < right:
            cur_area = (right - left) * min(height[left], height[right])
            max_area = max(cur_area, max_area)
            if height[left] > height[right]:
                right -= 1
            else:
                left += 1
        return max_area

优化后答案

class Solution:
    def maxArea(self, height: List[int]) -> int:
        max_area = 0
        left = 0
        right = len(height) - 1
        
        while left < right:
            # 计算当前容器的水量
            current_area = min(height[left], height[right]) * (right - left)
            # 更新最大水量
            max_area = max(max_area, current_area)
            
            # 移动较短的那根柱子对应的指针
            if height[left] < height[right]:
                current_left = height[left]
                # 跳过计算，直到找到一个更高的柱子
                while left < right and height[left] <= current_left:
                    left += 1
            else:
                current_right = height[right]
                # 跳过计算，直到找到一个更高的柱子
                while left < right and height[right] <= current_right:
                    right -= 1
                    
        return max_area