108. Convert Sorted Array To Binary Search Tree (Easy) 降有序数组转换为二叉搜索树

题干

Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.

A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.

Example 1:

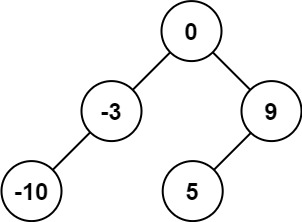
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:

Example 2:

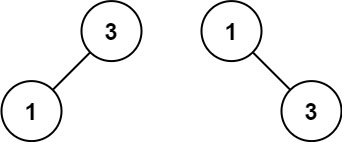
Input: nums = [1,3]
Output: [3,1]
Explanation: [1,null,3] and [3,1] are both height-balanced BSTs.

Constraints:

• 1 <= nums.length <= 104
• -104 <= nums[i] <= 104
• nums is sorted in a strictly increasing order.

解法

朴素解法

有序数组，组成高度平衡的二叉搜索树。重点就在于找到中间值，然后左右区间分别构造二叉树的左右子树。

递归解法

• 输入参数：输入一个数组
• 输出参数：输出一个二叉树节点
• 终止条件：
  • 当数组长度等于1时，返回二叉树节点，值等于元素，左右子节点等于None
• 单层核心逻辑：
  • 当前数组长度整除2，结果就是中间值的index
  • 将当前中间值作为value
  • 分别把左区间[0:index]和右区间[index+1:]的返回值，当作当前节点的左右子节点

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> Optional[TreeNode]:
        len_nums = len(nums)
        if len_nums < 1:
            return None
        elif len_nums == 1:
            return TreeNode(nums[0])
        root_i = len_nums // 2
        root = TreeNode(nums[root_i])
        root.left = self.sortedArrayToBST(nums[:root_i])
        root.right = self.sortedArrayToBST(nums[root_i+1:])
        return root

543. Diameter Of Binary Tree [Easy] 二叉树的直径

题干

Given the root of a binary tree, return *the length of the diameter of the tree*.

The diameter of a binary tree is the length of the longest path between any two nodes in a tree. This path may or may not pass through the root.

The length of a path between two nodes is represented by the number of edges between them.

Example 1:

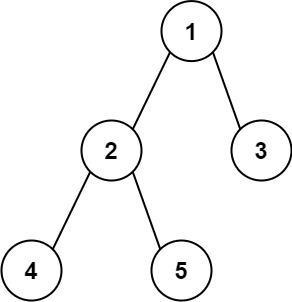
Input: root = [1,2,3,4,5]
Output: 3
Explanation: 3 is the length of the path [4,2,1,3] or [5,2,1,3].

Example 2:

Input: root = [1,2]
Output: 1

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -100 <= Node.val <= 100

解法

递归解法

核心思路：

• 将问题转换为求每个节点的左右子树高度之和，后序遍历

递归实现（返回节点高度，同时计算递归过程中各个节点的最长直径；这两者都是后序遍历，所以可以循只遍历一次）：

• 输入参数：Optional[TreeNode]
• 输出参数：int（高度）
• 终止条件：None节点的高度为0，返回它
• 单层核心逻辑：
  • 返回节点高度
  • 计算左节点的高度，计算右节点的高度
  • 取最大值+1，并返回
  • 更新全局最长直径

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def diameterOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        self.max_diameter = 0
        self.getHeight(root)
        return self.max_diameter
    
    def getHeight(self, node: Optional[TreeNode]) -> int:
        # 终止条件
        if node is None:
            return 0
        # 后序遍历
        left_h = self.getHeight(node.left)
        right_h = self.getHeight(node.right)
        self.max_diameter = max(left_h + right_h, self.max_diameter)
        return 1 + max(left_h, right_h)

101. Symmetric Binary Tree (Easy) 对称二叉树

题干

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

Example 1:

Input: root = [1,2,2,3,4,4,3]
Output: true

Example 2:

Input: root = [1,2,2,null,3,null,3]
Output: false

Constraints:

• The number of nodes in the tree is in the range [1, 1000].
• -100 <= Node.val <= 100

Follow up: Could you solve it both recursively and iteratively?

解法

递归解法

核心思路：将根节点的左右子树递归对称对比，单个节点的对比包含以下规则：

• 两个节点都为None的时候，是对称的
• 两个节点只有一个是None的时候，不对称
• 两个节点都不是None，value不相同的时候，不对称
• 两个节点都不是None，节点value相同，并且左右子树递归对称的时候，对称

递归实现：

• 输入参数：两个Optional[TreeNode]
• 输出参数：bool
• 终止条件：
  • 两个节点都是None，返回True
  • 只有一个是None，返回False
  • 两个节点不为None，value不同，返回False
• 单层核心逻辑：
  • 节点1的左子树和节点2的右子树对比
  • 节点1的右子树和节点2的左子树对比
  • 节点1和节点2的对比

两个节点的val对比属于终止条件，并不是中节点的比较，因为节点的比较，除了val之外，还有left和right的对比。

单层核心逻辑，左右中是后序遍历。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSymmetric(self, root: Optional[TreeNode]) -> bool:
        if root is None:
            return True
        return self.isSame(root.left, root.right)
    
    def isSame(self, node_01: Optional[TreeNode], node_02: Optional[TreeNode]) -> bool:
        # 终止条件
        if not node_01 and not node_02:
            return True
        if not node_01 or not node_02:
            return False
        if node_01.val != node_02.val:
            return False
        
        # 后序处理，左右中（中隐藏在return的逻辑里面了）
        # 注意，中是指中节点，当前节点的val对比并不是中节点完整的逻辑对比，所以不算中
        if not self.isSame(node_01.left, node_02.right):
            return False
        if not self.isSame(node_01.right, node_02.left):
            return False
        return True

226. Revert Binary Tree (Easy) 反转二叉树

题干

Given the root of a binary tree, invert the tree, and return its root.

Example 1:

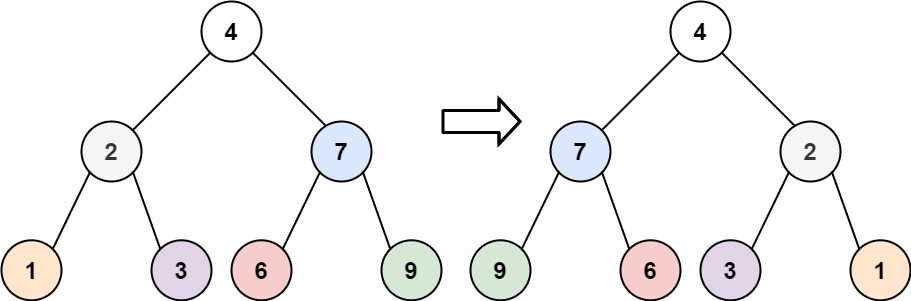
Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Example 2:

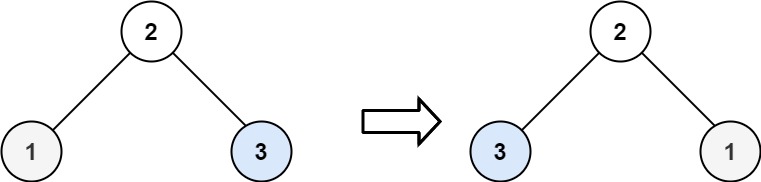
Input: root = [2,1,3]
Output: [2,3,1]

Example 3:

Input: root = []
Output: []

Constraints:

• The number of nodes in the tree is in the range [0, 100].
• -100 <= Node.val <= 100

解法

递归解法

核心思想：使用前序或后序遍历来处理。

中序遍历不行的原因是，在左和右子树分别处理完之前，就把中的逻辑（交换左右子树）处理了，相当于左右子树发生了改变，逻辑会比较绕。

递归实现：

• 输入参数：Optional[TreeNode]
• 输出参数：空
• 终止条件：如果传入参数为None，返回
• 单层核心逻辑：按照前序或者后序遍历处理

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def invertTree(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
        self.invertNode(root)
        return root
        
    def invertNode(self, node: Optional[TreeNode]):
        if node is None:
            return
        # 前序遍历
        # 处理`中`，交换左右子树
        node.left, node.right = node.right, node.left
        # 递归处理左子树
        self.invertNode(node.left)
        # 递归处理右子树
        self.invertNode(node.right)

104. Maximum Depth Of Binary Tree (Easy) 栈的最大深度

题干

Given the root of a binary tree, return its maximum depth.

A binary tree’s maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

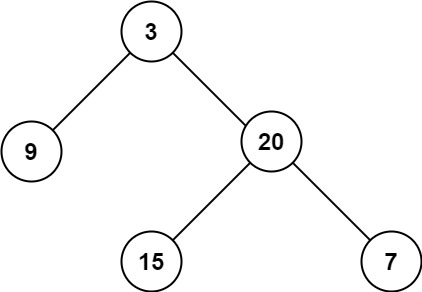
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Constraints:

• The number of nodes in the tree is in the range [0, 104].
• -100 <= Node.val <= 100

解法

递归解法

核心思想：求最大深度，其实就是求root的高度。求高度使用的是后序遍历，左右中

左右中，最后处理中，才能递归把左和右的结果，拿来给中用。

为什么不使用前序遍历，中左右，来直接求深度呢？因为无法让下层节点利用上层节点来递归

递归实现：

• 输入参数：Optional[node]
• 输出参数：int(高度)
• 结束条件：如果传入的node为空，则返回0（最下层元素的高度是1，那么None的就是0）
• 单层核心逻辑：递归求左右子节点的高度，然后将较大的值加上1，就是当前节点的高度

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        return self.getHeight(root)
    
    def getHeight(self, node: Optional[TreeNode]) -> int:
        # 终止条件
        if node is None:
            return 0

        # 单层核心逻辑
        # 以下四条语句，可以合并为最后一条语句
        # left_height = self.getHeight(node.left)
        # right_height = self.getHeight(node.right)
        # cur_height = max(left_height, right_height) + 1
        # return cur_height
        return 1 + max(self.getHeight(node.left), self.getHeight(node.right))

94. Binary Tree Inorder Traversal (Easy) 二叉树的中序遍历

题干

Given the root of a binary tree, return the inorder traversal of its nodes’ values.

Example 1:

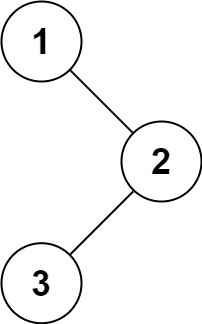
Input: root = [1,null,2,3]
Output: [1,3,2]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [1]
Output: [1]

Constraints:

• The number of nodes in the tree is in the range [0, 100].
• -100 <= Node.val <= 100

Follow up: Recursive solution is trivial, could you do it iteratively?

解法

递归解法

中序遍历，就是左中右这种顺序

• 输入参数：node节点，保存结果的列表
• 输出参数：空
• 结束条件：当node是None的时候直接返回
• 单层关键逻辑：当node不是None的时候，先处理左节点（需递归），将结果加入到结果，然后是中节点（当前节点，无需递归），然后时右节点（需递归）。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        res = []
        self.traversal(root, res)
        return res
    
    def traversal(self, node: Optional[TreeNode], res: List[int]):
        if node is None:
            return
        
        self.traversal(node.left, res)
        res.append(node.val)
        self.traversal(node.right, res)

栈解法

中序遍历，就是左中右顺序。

• 栈中保存需要后序处理的节点（当前节点的左子树上所有的左节点），直到当前节点为None
• 从栈中弹出元素，记录当前元素的值，然后使用当前节点的right节点当作当前节点，进入下次循环

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        answer: List[int] = []
        st_node: List[int] = []
        cur_node = root

        # 中序遍历：左中右
        # 左子树依序入栈，到底后逐个弹出，处理中和右
        while cur_node or st_node:
            # 先处理当前节点的左子树
            while cur_node:
                st_node.append(cur_node)
                cur_node = cur_node.left

            # 将栈顶元素弹出栈（左节点首先会在栈顶）
            cur_node = st_node.pop()
            answer.append(cur_node.val)

            # 若无right，cur_node为None，会在下个循环中重新pop一个
            cur_node = cur_node.right
        
        return answer

二叉树的定义

在电脑科学中，二叉树（英语：Binary tree）是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构[1]。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。

二叉树的第i层至多拥有2i−1个节点；深度为k的二叉树至多总共有2k+1−1个节点（定义根节点所在深度 k0=0!），而总计拥有节点数符合的，称为“满二叉树”；深度为k有n个节点的二叉树，当且仅当其中的每一节点，都可以和深度k的满二叉树，序号1到n的节点一对一对应时，称为完全二叉树。对任何一棵非空的二叉树T，如果其叶片（终端节点）数为n0，分支度为2的节点数为n2，则n0=n2+1。

二叉树的发展历史

1. 早期背景和数学基础：
   • 在计算机科学发展之前，树结构的概念已经在数学中存在。数学家和图论专家研究了树的性质和特点。
   • 计算机科学的发展从20世纪中期开始，数据结构和算法的研究逐渐兴起。
2. 20世纪50年代：
   • 二叉树在计算机科学中开始被正式研究和应用。1950年代是二叉树概念的形成时期。
   • 当时的计算机科学家开始研究如何有效地存储和检索数据，二叉树被发现是一种有效的数据结构，尤其是在实现搜索和排序操作时。
3. 二叉搜索树 (BST)：
   • 二叉搜索树是一种特殊的二叉树，其中左子节点的值总是小于父节点的值，右子节点的值总是大于父节点的值。
   • 1959年，二叉搜索树的概念被正式提出，成为一种广泛使用的数据结构，用于高效的数据查找和排序。
4. 自平衡二叉树：
   • 1962年，G.M. Adelson-Velsky 和 E.M. Landis 提出了 AVL树，这是第一种自平衡二叉搜索树。AVL树通过在插入和删除节点时进行旋转操作，保持树的平衡，从而保证了操作的时间复杂度为O(log n)。
   • 1972年，Rudolf Bayer 发明了红黑树，这是一种自平衡二叉搜索树，进一步提高了效率和稳定性。
5. 其他变体和应用：
   • 随着计算机科学的发展，二叉树的其他变体（如堆、B树、Trie树等）被广泛研究和应用在不同的领域，如数据库、编译器、网络路由等。
   • 二叉树在算法设计、数据压缩（如哈夫曼编码）、表达式解析和计算等方面有着广泛的应用。

二叉树的种类

根据结构和性质的不同，二叉树可以分为许多种类。以下是一些常见的二叉树种类及其特点：

1. 完全二叉树（Complete Binary Tree）

• 定义：除了最后一层外，其他每一层的节点数都达到最大，且最后一层的节点都集中在最左边。
• 特点：叶子节点只能出现在最后两层，并且最后一层的叶子节点都靠左排列。

1. 满二叉树（Full Binary Tree）

• 定义：每个节点要么有两个子节点，要么没有子节点。
• 特点：叶子节点都在同一层，且每个非叶子节点都有两个子节点。

1. 平衡二叉树（Balanced Binary Tree）

• 定义：任意节点的左右子树的高度差不超过1。
• 特点：为了保证查找、插入和删除操作的时间复杂度保持在 O(log n) 级别。

1. 二叉搜索树（Binary Search Tree，BST）

• 定义：对任意节点，左子树上所有节点的值都小于该节点的值，右子树上所有节点的值都大于该节点的值。
• 特点：支持高效的查找、插入和删除操作。

总结 二叉树还有很多其他种类，每种都有其特定的用途和性质。根据具体应用场景选择合适的二叉树可以提高算法的效率和性能。

二叉树的重要性

• 高效查找：二叉搜索树允许在平均O(log n)的时间内进行查找操作。
• 排序功能：通过中序遍历二叉搜索树，可以获得有序的数据序列。
• 灵活性和扩展性：二叉树的变体（如AVL树、红黑树、B树等）在保持效率的同时，适应不同的应用场景和需求。
• 基础性：二叉树是很多复杂数据结构和算法的基础，如图的遍历、表达式解析、哈夫曼编码等。

综上所述，二叉树作为一种基础的数据结构，在计算机科学的发展中起到了重要的作用。从最初的数学概念到如今各种复杂的变体和应用，二叉树一直是计算机科学研究和应用的核心部分。

二叉树在内存中的储存

二叉树在内存中，使用链式存储。

也有线性存储，即使用数组来存储。

假设我们在一个32位系统上，int 和指针都占用4个字节（32位）。我们将val设置为42，并假设left和right指针为空（即NULL）。

在二进制位模式下：

• 42 的二进制表示是 00000000 00000000 00000000 00101010。
• NULL 的二进制表示是 00000000 00000000 00000000 00000000。

因此，内存布局将是：

地址:    0x1000   0x1004   0x1008   0x100C
        +--------+--------+--------+--------+
值:     |   42   |  NULL  |  NULL  |
        +--------+--------+--------+--------+
字段:   |  val   |  left  |  right |
        +--------+--------+--------+--------+

64位系统中，val值不够长度会进行补齐，保持长度和后面的指针一致。

21. Merge Two Sorted List (Easy) 合并有序链表

题干

You are given the heads of two sorted linked lists list1 and list2.

Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.

Return the head of the merged linked list.

Example 1:

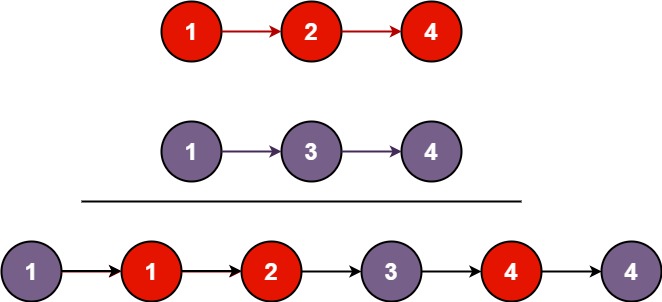
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]

Example 2:

Input: list1 = [], list2 = []
Output: []

Example 3:

Input: list1 = [], list2 = [0]
Output: [0]

Constraints:

• The number of nodes in both lists is in the range [0, 50].
• -100 <= Node.val <= 100
• Both list1 and list2 are sorted in non-decreasing order.

解法

朴素解法

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
        pre = ListNode()
        tail = pre

        while list1 is not None and list2 is not None:
            if list1.val > list2.val:
                tail.next = list2
                list2 = list2.next
            else:
                tail.next = list1
                list1 = list1.next
            tail = tail.next
        tail.next = list1 if list1 is not None else list2
        return pre.next

• 使用一个pre节点，避免了处理第一个节点的特殊情况
• while循环只处理两个链表都没到尾部的情况，其他一个到尾部时单独处理，这样避免了重复判断None的语句。

206. Reverse Linked List (Easy) 反转链表

题干

Given the head of a singly linked list, reverse the list, and return the reversed list.

Example 1:

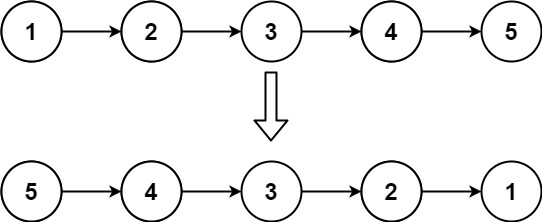
Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]

Example 2:

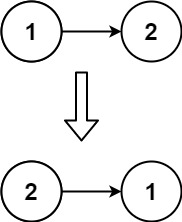
Input: head = [1,2]
Output: [2,1]

Example 3:

Input: head = []
Output: []

Constraints:

• The number of nodes in the list is the range [0, 5000].
• -5000 <= Node.val <= 5000

Follow up: A linked list can be reversed either iteratively or recursively. Could you implement both?

解法

朴素解法（双指针）

第一个元素指向None，然后后续元素逐个指向前一个元素，完毕

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        pre = None
        cur = head
        while cur:
            next_node = cur.next
            cur.next = pre
            pre, cur = cur, next_node
        return pre

• Time Cost: O(n)
• Space Cost: O(1)

递归解法

其实还是双指针，只是换了递归的写法

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:
    def reverseList(self, head: Optional[ListNode]) -> Optional[ListNode]:
        return self.reverse(None, head)

    def reverse(self, pre: Optional[ListNode], cur: Optional[ListNode]) -> Optional[ListNode]:
        if cur == None:
            return pre
        temp = cur.next
        cur.next = pre
        return self.reverse(cur, temp)

141. Linked List Cycle (Easy) 环形链表

题干

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

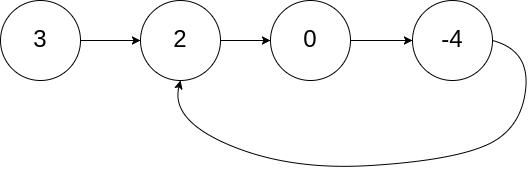
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

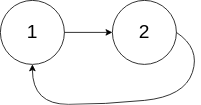
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 104].
• -105 <= Node.val <= 105
• pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

解法

朴素解法

使用一个备忘录，记录每个节点，若后面有重复，即节点存入前，节点已经存在。那么就有环形存在

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        temp: List[ListNode] = []
        while head is not None:
            if head in temp:
                return True
            temp.append(head)
            head = head.next
        return False

• Time Cost: O(n^2)
• Space Cost: O(n)

优化解法

基于朴素解法，只是数据结构换成了dict

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

class Solution:
    def hasCycle(self, head: Optional[ListNode]) -> bool:
        temp: Dict[ListNode, int] = {}
        while head is not None:
            if head in temp:
                return True
            temp[head] = 0
            head = head.next
        return False